
This pattern indicates that the variances of the residuals are unequal (nonconstant). Notice that, as the value of the fits increases, the scatter among the residuals widens. The variance of the residuals increases with the fitted values. Consider removing data values that are associated with abnormal, one-time events (special causes). Correct any data entry or measurement errors. You should try to identify the cause of any outlier. If there are too many outliers, the model may not be acceptable. One of the points is much larger than all of the other points. The following graphs show an outlier and a violation of the assumption that the residuals are constant. If the p-value is larger than the significance level, the test does not detect any lack-of-fit. P-value > α: The lack-of-fit is not statistically significant To improve the model, you may need to add terms or transform your data. P-value ≤ α: The lack-of-fit is statistically significant If the p-value is less than or equal to the significance level, you conclude that the model does not correctly specify the relationship. A significance level of 0.05 indicates a 5% risk of concluding that the model correctly specifies the relationship between the response and the predictors when the model does not. Usually, a significance level (denoted as alpha or α) of 0.05 works well. The null hypothesis for the lack-of-fit test is that the model correctly specifies the relationship between the response and the predictors. To determine whether the model correctly specifies the relationship between the response and the predictors, compare the p-value for the lack-of-fit test to your significance level to assess the null hypothesis. The more DF for pure error, the greater the power of the lack-of-fit test. The lack-of-fit test uses the degrees of freedom for lack-of-fit. The DF for lack-of-fit allow a test of whether the model form is adequate. If the two conditions are met, then the two parts of the DF for error are lack-of-fit and pure error. For example, if you have 3 observations where pressure is 5 and temperature is 25, then those 3 observations are replicates. Replicates are observations where each predictor has the same value. The second condition is that the data contain replicates.

If the model does not include the quadratic term, then a term that the data can fit is not included in the model and this condition is met.
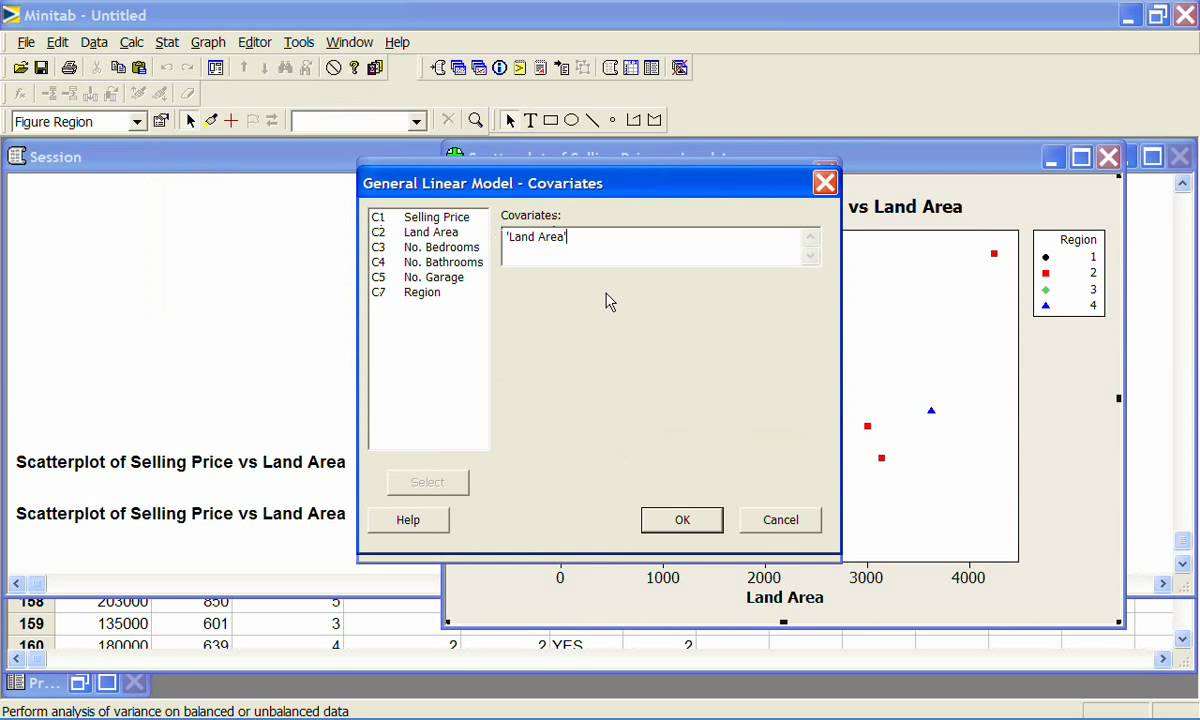
For example, if you have a continuous predictor with 3 or more distinct values, you can estimate a quadratic term for that predictor. The first condition is that there must be terms you can fit with the data that are not included in the current model.

If two conditions are met, then Minitab partitions the DF for error. Increasing the number of terms in your model uses more information, which decreases the DF available to estimate the variability of the parameter estimates. Increasing your sample size provides more information about the population, which increases the total DF.
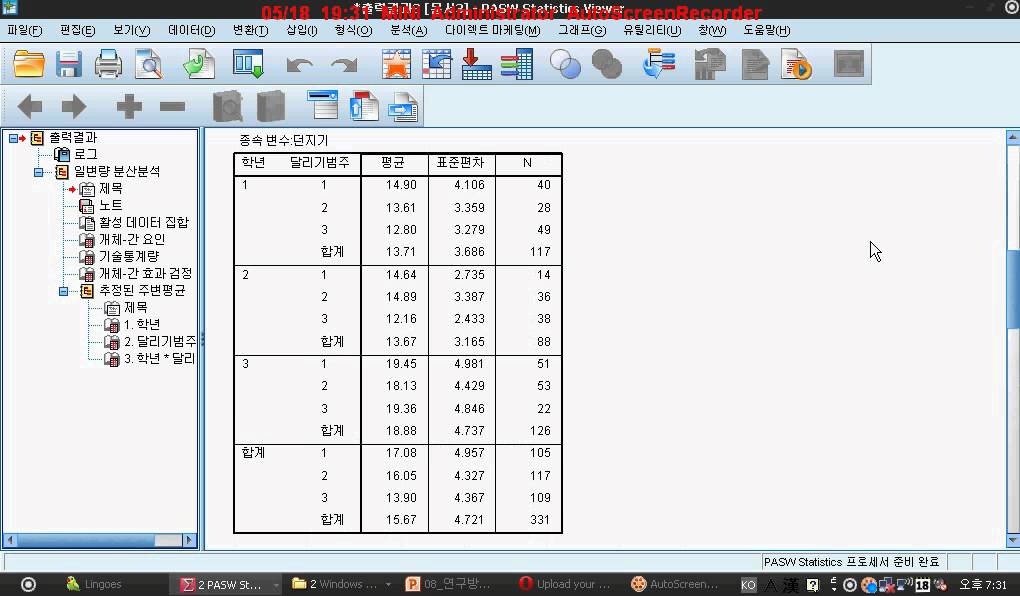
The DF for a term show how much information that term uses. The total DF is determined by the number of observations in your sample. The analysis uses that information to estimate the values of unknown population parameters. The total degrees of freedom (DF) are the amount of information in your data.


 0 kommentar(er)
0 kommentar(er)
